Randomized Attention: a Generalized Random Feature Attention Algorithm

A blog post on novel perspectives to understand random feature attention

$$ \definecolor{strings}{rgb}{.824,.251,.259} \definecolor{keywords}{rgb}{.224,.451,.686} \definecolor{comment}{rgb}{.322,.451,.322} \newcommand{\norm}[1]{\left\lVert#1\right\rVert} \newcommand{\coloneqq}{\mathrel{\vcenter{:}}=} \newcommand{\R}{\mathbb{R}} \newcommand{\mathbold}[1]{\boldsymbol{\mathbf{#1}}} \newcommand{\mcK}{\mathcal{K}} \newcommand{\mcN}{\mathcal{N}} \newcommand{\mcO}{\mathcal{O}} \newcommand{\mcP}{\mathcal{P}} \newcommand{\mcC}{\mathcal{C}} \newcommand{\mcS}{\mathcal{S}} \newcommand{\mcL}{\mathcal{L}} \newcommand{\mba}{\mathbold{a}} \newcommand{\mbb}{\mathbold{b}} \newcommand{\mbc}{\mathbold{c}} \newcommand{\mbd}{\mathbold{d}} \newcommand{\mbe}{\mathbold{e}} \newcommand{\vf}{\mathbold{f}} \newcommand{\mbg}{\mathbold{g}} \newcommand{\mbh}{\mathbold{h}} \newcommand{\mbi}{\mathbold{i}} \newcommand{\mbj}{\mathbold{j}} \newcommand{\mbk}{\mathbold{k}} \newcommand{\mbl}{\mathbold{l}} \newcommand{\mbm}{\mathbold{m}} \newcommand{\mbn}{\mathbold{n}} \newcommand{\mbo}{\mathbold{o}} \newcommand{\mbp}{\mathbold{p}} \newcommand{\mbq}{\mathbold{q}} \newcommand{\mbr}{\mathbold{r}} \newcommand{\mbs}{\mathbold{s}} \newcommand{\mbt}{\mathbold{t}} \newcommand{\mbu}{\mathbold{u}} \newcommand{\mbv}{\mathbold{v}} \newcommand{\mbw}{\mathbold{w}} \newcommand{\mbx}{\mathbold{x}} \newcommand{\mby}{\mathbold{y}} \newcommand{\mbz}{\mathbold{z}} \newcommand{\mbA}{\mathbold{A}} \newcommand{\mbB}{\mathbold{B}} \newcommand{\mbC}{\mathbold{C}} \newcommand{\mbD}{\mathbold{D}} \newcommand{\mbE}{\mathbold{E}} \newcommand{\mbF}{\mathbold{F}} \newcommand{\mbG}{\mathbold{G}} \newcommand{\mbH}{\mathbold{H}} \newcommand{\mbI}{\mathbold{I}} \newcommand{\mbJ}{\mathbold{J}} \newcommand{\mbK}{\mathbold{K}} \newcommand{\mbL}{\mathbold{L}} \newcommand{\mbM}{\mathbold{M}} \newcommand{\mbN}{\mathbold{N}} \newcommand{\mbO}{\mathbold{O}} \newcommand{\mbP}{\mathbold{P}} \newcommand{\mbQ}{\mathbold{Q}} \newcommand{\mbR}{\mathbold{R}} \newcommand{\mbS}{\mathbold{S}} \newcommand{\mbT}{\mathbold{T}} \newcommand{\mbU}{\mathbold{U}} \newcommand{\mbV}{\mathbold{V}} \newcommand{\mbW}{\mathbold{W}} \newcommand{\mbX}{\mathbold{X}} \newcommand{\mbY}{\mathbold{Y}} \newcommand{\mbZ}{\mathbold{Z}} \newcommand{\mbphi}{\mathbold{\phi}} $$

Overview

This blog post introduces a new perspective to understanding the Random Feature Attention (RFA) mechanism. We show that 1) the conventional softmax attention can be equivalently rewritten as an expectation over RFAs, and that 2) RFA is in fact a self-normalized importance sampler to estimate conventional softmax attention. This new perspective grounds the heuristic RFA approximation and also sheds light on how to generalize further and improve RFAs. More details can be found in our ICML paper .

Attention

The attention mechanism has become a ubiquitous building block in modern deep learning models and brought great success across various domains, including natural language processing (NLP), computer vision (CV), bioinformatics, reinforcement learning, etc. Attention mechanisms take three different kinds of inputs: a set of $N$ query vectors $\mbQ \in \R^{N \times D}$, $M$ key vectors $\mbK \in \R^{M \times D}$ and value vectors $\mbV \in \R^{M \times D}$. In this work we focus on self-attention, where $M=N$ and all of queries, keys and values are obtained by projecting tokens of the same input sequence.

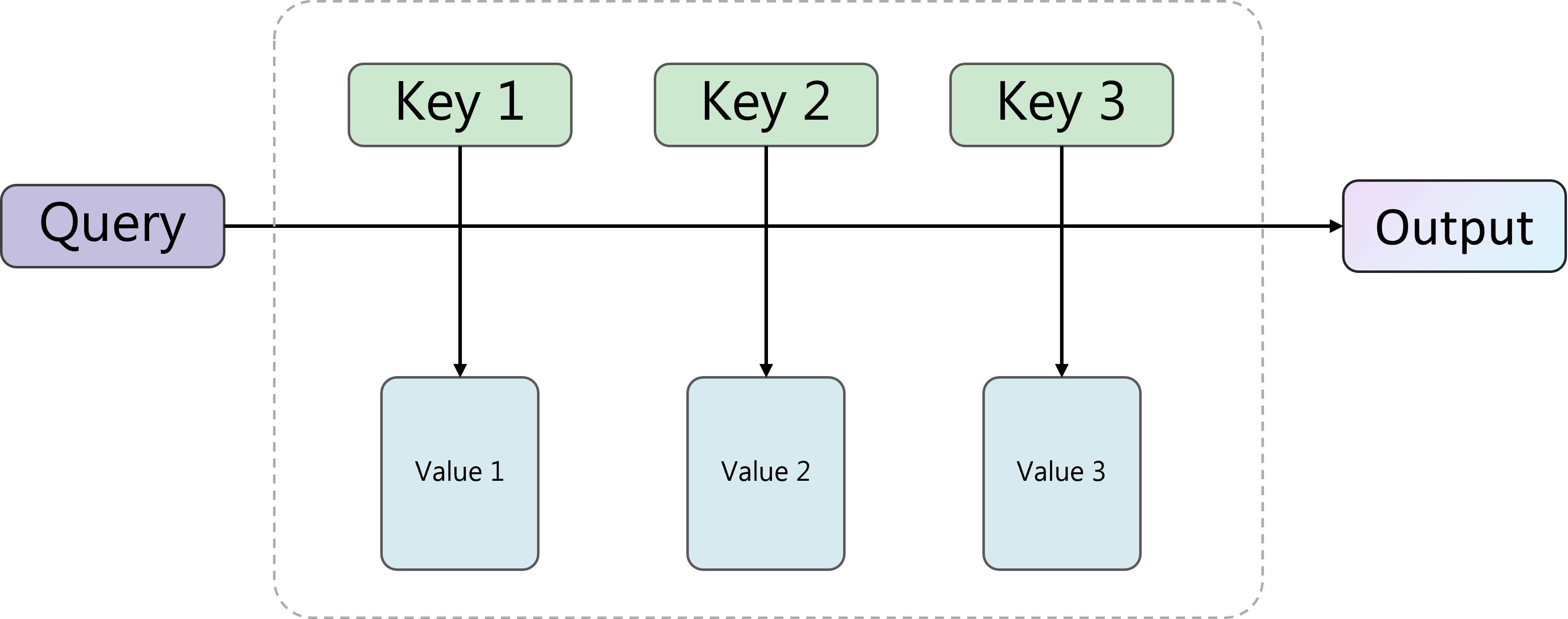
For each query $\mbq_n$, conventional softmax attention computes the following quantity, We omit the commonly used scaling factor $1 / \sqrt{d}$ for simplicity as it can be merged into the computation of queries or keys. \begin{equation} \mathsf{SoftmaxAttn}\left(\mbq_{n},\mbK,\mbV\right)\coloneqq\sum_{m=1}^M\frac{\exp\left(\mbq_{n}^\top \mbk_{m} \right)}{\sum_{m’=1}^M \exp\left(\mbq_{n}^\top \mbk_{m’} \right)} \mbv_{m}^{\top}. \end{equation} Intuitively, softmax attention first compares the query against each key and then computes the average over value vectors weighted by the normalized query-key similarities. It is effective in capturing long-term dependencies across sequence elements and producing contextualized representations; however, it suffers from quadratic time and memory complexity due to the explicit computation of all $NM$ query-key pairs.

Random Feature Attention

To reduce the computational complexity of softmax attention, researchers proposed to use random features (RF) to linearize softmax attention. In particular, they make use of the following identity to rewrite the exponential kernel as an expectation, \begin{equation} \exp(\mbx^\top \mby) = \mathbb{E}_{\omega \sim \mathcal{N}(\omega;0,\mathbf{I})}\left[\xi(\mbx,\omega)^\top\xi(\mby, \omega)\right], \label{eqn:identity} \end{equation} where $\xi(\cdot, \cdot): \R^D \times \R^D \rightarrow \R^l$, $l\geq 1$, is a non-linear randomized mapping projecting the input vector to a $l$-dimensional vector via a randomly drawn $\omega \sim \mathcal{N}(\omega;0,\mathbf{I})$. There are several parameterization choices of $\xi(\mbx,\omega)$ for the identity to hold; in this work we focus on the positive type $\xi(\mbx,\omega) = \exp{\left(\omega^\top \mbx - \frac{1}{2}\norm{\mbx}^2\right)}$ as proposed in . A classical choice of randomized mappings is to let $\xi(\mbx,\omega) = \exp{\left( \frac{1}{2}\norm{\mbx}^2\right)}\left[\sin{\left(\omega^\top \mbx\right)},\cos{\left(\omega^\top \mbx\right)}\right]^\top$ . Besides, there are other advanced randomized mappings enjoying more appealing properties; see for a more in-depth study.

To estimate the expectation in \eqref{eqn:identity}, one can draw multiple Monte Carlo samples from $\mathcal{N}(\omega;0,\mathbf{I})$ such that $\exp(\mbx^{\top} \mby) \approx \frac{1}{S}\sum_{s=1}^S \xi(\mbx,\omega_s)^{\top}\xi(\mby, \omega_s)$. By substituting such approximation into the softmax attention, we obtain random feature attention (RFA) (also called Performer ), $$ \begin{align} \frac{\sum_{m=1}^M\exp\left(\mbq_{n}^\top \mbk_{m} \right)\mbv_{m}^{\top}}{\sum_{m'=1}^M \exp\left(\mbq_{n}^\top \mbk_{m'} \right)} &\approx \frac{\sum_{m=1}^M \sum_{s=1}^S\xi(\mbq_n,\omega_s)^{\top}\xi(\mbk_m, \omega_s)\mbv_{m}^{\top}}{\sum_{m'=1}^M\sum_{s=1}^S \xi(\mbq_n,\omega_s)^{\top}\xi(\mbk_{m'}, \omega_s)} \notag \\ &=\frac{ \sum_{s=1}^S\xi(\mbq_n,\omega_s)^{\top}\sum_{m=1}^M\xi(\mbk_m, \omega_s)\mbv_{m}^{\top}}{\sum_{s=1}^S \xi(\mbq_n,\omega_s)^{\top}\sum_{m'=1}^M\xi(\mbk_{m'}, \omega_s)} \label{eqn:rfa}\\ &\coloneqq \mathsf{RFA}\left(\mbq_{n},\mbK,\mbV\right) \notag. \end{align} $$ Thanks to the linearized formulation, one can first pre-compute the corresponding key-value statistics $\sum_{m=1}^M\xi(\mbk_{m},\omega_s)\mbv_{m}^{\top}$ and $\sum_{m=1}^M\xi(\mbk_{m},\omega_s)$ once, and then reuse them for each query. Consequently, it achieves linear complexity in both time and memory with respect to the sequence length.

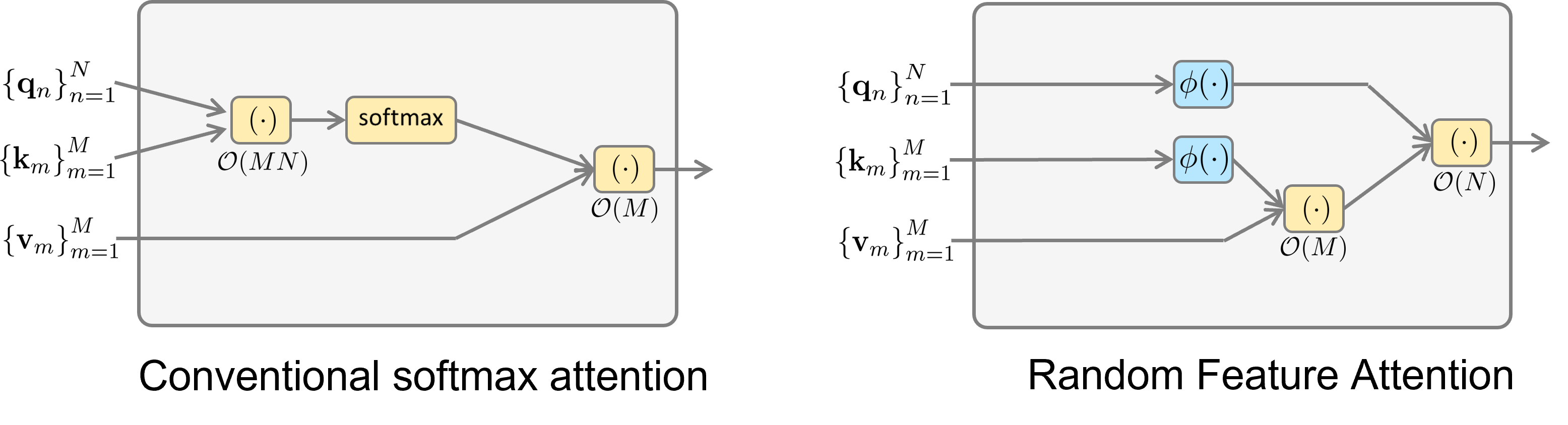
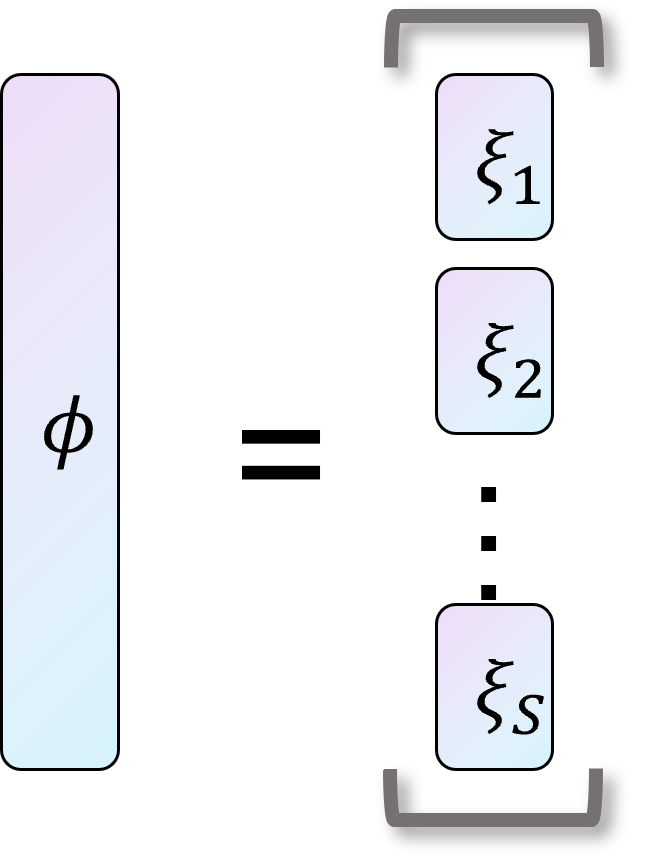
Why it is called random feature attention?
This is due to the fact that the sample average can be written as $\mbphi(\mbx,\mbw)^\top \mbphi(\mby,\mbw)$, where $\mbphi(\mbx,\mbw) \coloneqq 1/\sqrt{S}[\xi(\mbx,\omega_1), \dots, \xi(\mbx, \omega_S)]^\top \in \R^{lS}$. The $\mbphi(\cdot,\cdot)$ can be considered as a feature map transforming the input vector to a new vector representation; as a result, $\mbphi(\cdot,\cdot)$ are conveniently referred to as random features .

The Biasedness of RFA

RFA suffers from significant performance degradation across various tasks, as observed in many previous studies (e.g., see here). Although computationally efficient, the reduced modeling capacity of RFA greatly limits its practical usage. Researchers try to improve the performance from different perspectives, such as

• developing better random feature types ,
• connecting it with fast weight programmers ,
• incorporating relative information , and so on.

In this work, we explore an orthogonal axis by re-examining the estimation bias of RFA. Our key observation is that RFA is a heuristic approximation to the whole softmax attention. Although the estimation of individual exponential kernels is unbiased, such estimation of a ratio of exponential kernels is not unbiased anymore. This is due to the non-linearity of ratios,

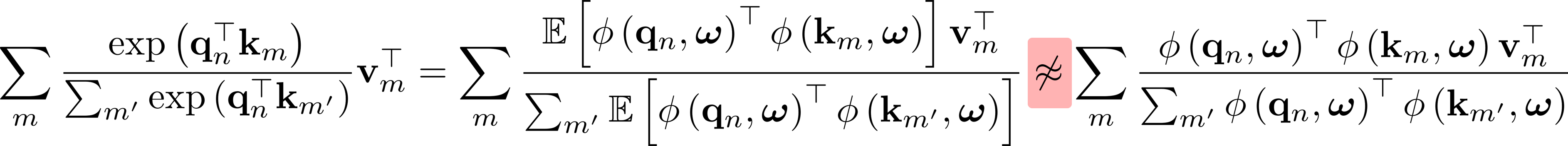
Such bias not only incurs a potentially large approximation gap between RFA and softmax attention but also bottlenecks the effectiveness of unbiased kernel estimation.

Our work aims to address the following research question:
Given that we already know how to unbiasedly estimate exponential kernels, how do we construct an unbiased estimator for the whole softmax attention?

Randomized Attention: An Unbiased Estimator for Softmax Attention

We answer this question in the affirmative and prove that softmax attention can be rewritten as an expectation of simple RFAs, $$ \begin{equation} \mathsf{SoftmaxAttn}(\mbq_n, \mbK,\mbV) = \sum_{m} \frac{\exp \left(\mathbf{q}_{n}^\top \mathbf{k}_{m} \right)}{\sum_{m'} \exp \left(\mathbf{q}_{n}^\top \mathbf{k}_{m'} \right)} \mathbf{v}_{m}^{\top} = \mathbb{E}_{p_n(\omega)}\left[f_n(\omega)\right],\label{eqn:softmax_as_expectation} \end{equation} $$ where $$ \begin{align} p_n(\omega) &= \sum_{m=1}^M \frac{\exp\left( \mbq_n^\top\mbk_m \right)}{\sum_{m'=1}^M\exp\left( \mbq_n^\top\mbk_{m'} \right)} \mathcal{N}(\omega; \mbq_n + \mbk_m, \mathbf{I}), \label{eqn:ra-density} \\ f_n(\omega) &= \frac{\xi(\mbq_n,\omega)^\top \sum_{m=1}^M \xi(\mbk_m, \omega) \mbv_{m}^{\top}}{\xi(\mbq_n,\omega)^\top \sum_{m'=1}^M \xi(\mbk_{m'}, \omega)} \label{eqn:ra-function}. \end{align} $$ Intuitively,

• $p_n(\omega)$ is a Gaussian mixture distribution whose component weights are exactly attention scores, while
• $f_n(\omega)$ is an RFA, except that the linearized similarity between queries and keys is computed via individual randomized mappings (or equivalently, one-dimensional random features).

Notably, our result can be viewed as a neat generalization of random feature approximation, which exhibits a high degree of symmetry: $$ \begin{align} \exp(\mbq_n^\top \mbk_m)\mbv_m^\top &= \mathbb{E}_{q(\omega)}\left[\xi(\mbq_n,\omega)^\top\xi(\mbk_m, \omega)\mbv_m^\top\right] \notag \\ \sum_{m} \frac{\exp \left(\mathbf{q}_{n}^\top \mathbf{k}_{m} \right)}{\sum_{m'} \exp \left(\mathbf{q}_{n}^\top \mathbf{k}_{m'} \right)} \mathbf{v}_{m}^{\top} &= \mathbb{E}_{p_n(\omega)}\left[\frac{\xi(\mbq_n,\omega)^\top \sum_{m=1}^M \xi(\mbk_m, \omega) \mbv_{m}^{\top}}{\xi(\mbq_n,\omega)^\top \sum_{m'=1}^M \xi(\mbk_{m'}, \omega)}\right].\notag \end{align} $$ Another implication is that we can construct a Monte Carlo estimator to approximate softmax attention in an unbiased way. By drawing $\omega_n \sim p_n(\omega)$, we obtain $$ \begin{align} \mathsf{SoftmaxAttn}(\mbq_n, \mbK,\mbV) &\approx \frac{\xi(\mbq_n,\omega_n)^\top \sum_{m=1}^M\xi(\mbk_m, \omega_n) \mbv_{m}^{\top}}{ \xi(\mbq_n,\omega_n)^\top \sum_{m'=1}^M\xi(\mbk_{m'}, \omega_n)} \label{eqn:ra}\\ &\coloneqq \mathsf{RA}\left(\mbq_{n},\mbK,\mbV\right) \notag \end{align} $$ We name such estimator Randomized Attention (RA) since it computes similarity scores with individual randomized mappings (instead of concatenated features). To the best of our knowledge, this is the first result that generalizes the unbiased kernel estimation to unbiased attention estimation.

Remark: The proof of \eqref{eqn:softmax_as_expectation} is done by first reverse-engineering the formulation of RFA, equating it with self-normalized importance sampling (see below) and then completing the square of Gaussians to derive the density $p_n(\omega)$. The function $f_n(\omega)$ can be solved by substituting the density $p_n(\omega)$ into the equation. See the paper for a detailed proof.

RFA as a Self-normalized Importance Sampler

The analysis above further reveals that RFA is a specific self-normalized importance sampling estimator to softmax attention.

Self-normalized Importance Sampling (SNIS)

Importance sampling (IS) is a general approach to approximating expectation $\mathbb{E}_{p_n(\omega)}\left[f_n(\omega)\right]$ when it is difficult to directly draw samples from $p_n(\omega)$. In importance sampling, we use a proposal distribution $q(\omega)$ to draw samples and estimate the quantity as $$ \mathbb{E}_{p_n(\omega)}\left[f_n(\omega)\right] = \mathbb{E}_{\omega \sim q(\omega)}\left[\frac{p_n(\omega)}{q(\omega)}f_n(\omega)\right] \approx \frac{1}{S} \sum_{s=1}^S \frac{p_n(\omega)}{q(\omega)} f_n(\omega_s), $$ where $\omega_1, \dots, \omega_S \sim q(\omega)$. The self-normalized importance sampling (SNIS) is defined as $$ \begin{equation} \mathbb{E}_{p_n(\omega)}\left[f_n(\omega)\right] \approx \frac{\sum_{s=1}^S\frac{p_n(\omega_s)}{q(\omega_s)}f(\omega_s)}{\sum_{s=1}^S\frac{p_n(\omega_s)}{q(\omega_s)}} = \sum_{s=1}^S\frac{\frac{p_n(\omega_s)}{q(\omega_s)}}{\sum_{s=1}^S\frac{p_n(\omega_s)}{q(\omega_s)}}f(\omega_s). \label{eqn:snis} \end{equation} $$ The name self-normalized comes from the fact that the importance weights $p_n(\omega)/q(\omega)$ are explicitly normalized and sum to 1.

RFA as SNIS

Our key finding here is that the formulation of RFA can be exactly derived from SNIS. Supposing $p_n(\omega)$ and $f_n(\omega)$ are given in \eqref{eqn:ra-density} and \eqref{eqn:ra-function} respectively, and $q(\omega) = \mathcal{N}(\omega;0,\mathbf{I})$, we have $$ \begin{align} \mathsf{RFA}\left(\mbq_{n},\mbK,\mbV\right) &= \frac{\sum_{s=1}^S\textcolor{strings}{\xi(\mbq_n,\omega_s)^{\top}\sum_{m=1}^M\xi(\mbk_m, \omega_s)\mbv_{m}^{\top}}}{\sum_{s=1}^S \textcolor{keywords}{\xi(\mbq_n,\omega_s)^{\top}\sum_{m'=1}^M\xi(\mbk_{m'}, \omega_s)}} = \frac{ \sum_{s=1}^S\textcolor{strings}{\frac{p_n(\omega_s)}{q(\omega_s)} f(\omega_s)}}{ \sum_{s=1}^S\textcolor{keywords}{\frac{p_n(\omega_s)}{q(\omega_s)}}}. \label{eqn:rfa-as-snis} \end{align} $$ This formulation provides a new understanding of RFA: it is just a specific instantiation of SNIS estimators for softmax attention, whose proposal distribution $q(\omega)$ is chosen to be standard Gaussian. This reveals one of the possible reasons why RFA does not work well in practice: The plain standard Gaussian proposal in RFA is far away from the true Gaussian mixture (as in RA), which might lead to a large approximation gap. More importantly, this view implies that we can generalize and extend RFA by using other proposal distributions or adopting other estimating schemes!

LARA: Generalizing Both RA and RFA

So far, we have two types of estimators available for approximating softmax attention: unbiased RA and biased RFA. Besides the theoretical biasedness, how do they differ in terms of practical modeling behavior? We list a comprehensive comparison to better illustrate their main differences.

• In terms of expressiveness:
  • ✔️ RA directly draws from the true distribution $p_n(\omega)$ \eqref{eqn:ra-density}. This makes the mechanism adaptive and query-specific, since the sampling distribution depends on the query vector. As a result, RA can specialize to each query and process the whole sequence at a finer-grained level.
  • ❌ RFA suffers from limited capacity, since there is a large discrepancy between the used proposal $q(\omega) = \mathcal{N}(\omega;0,\mathbf{I})$ and the true distribution $p_n(\omega)$; furthermore, $q(\omega)$ captures no contextual information, leading to low sample efficiency.
• In terms of efficiency:
  • ❌ RA suffers from quadratic computational costs. Since the sampling distribution is distinct for each query, we have to draw at least $\mathcal{O}(N)$ samples for all queries; at the same time, we needs to sum over all $M$ key-value pairs at each sampled $\omega_n$ (see \eqref{eqn:ra}), which leads to $\mathcal{O}(NM)$ complexity overall, as is the case for softmax attention;
  • ✔️ RFA uses SNIS to avoid computing or sampling from $p_n(\omega)$, which require quadratic-time computation. Drawing from a simpler proposal distribution allows samples to be shared across queries and still resulting in a $\mathcal{O}(M)$ complexity.

A diagram of LARA that combines the strengths of both approaches.

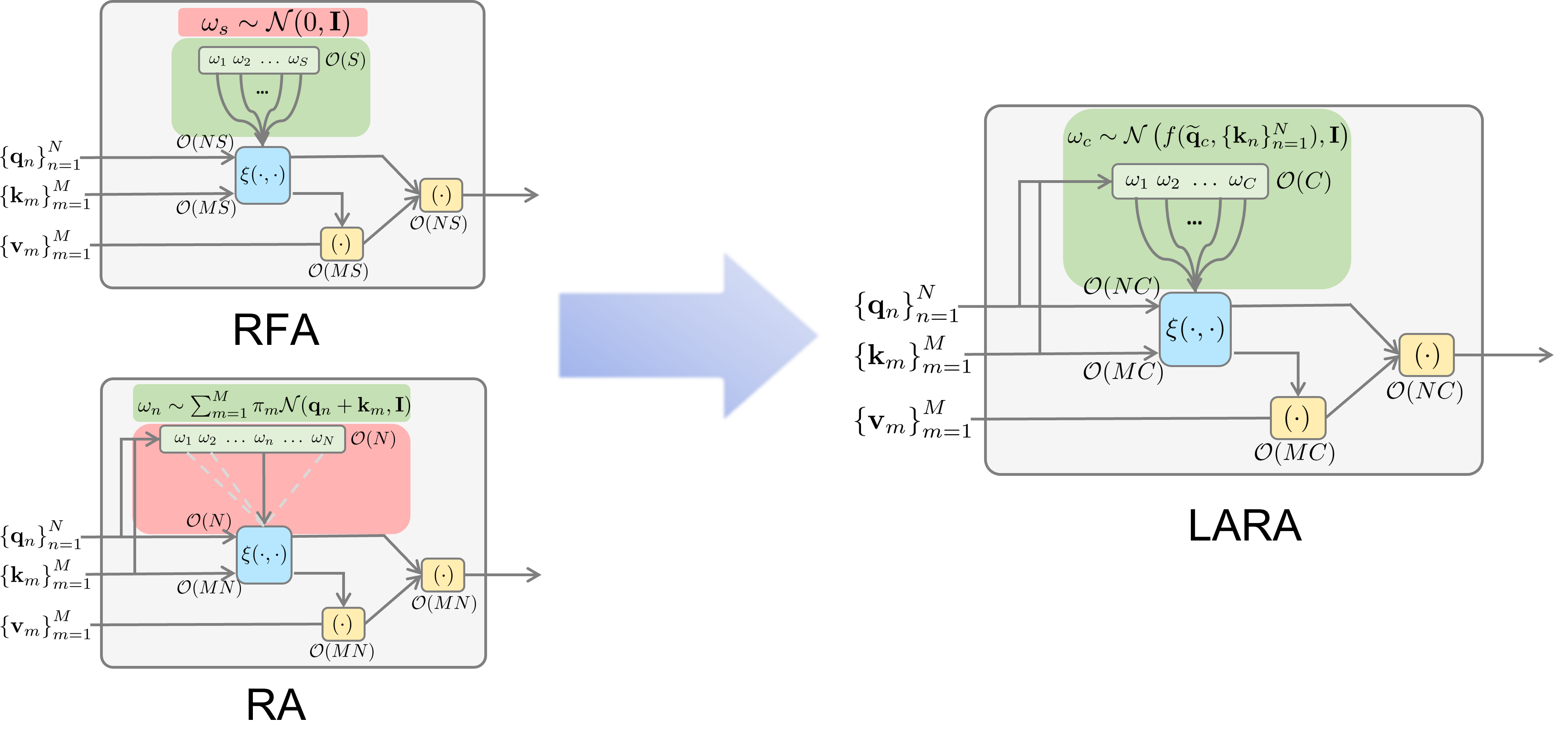
Motivated by the comparison, we propose LineAr-time Randomized Attention (LARA) that attempts to get the best of both worlds, combining both the efficiency of RFA and the expressiveness of RA.

• On the one hand, LARA inherits the SNIS formulation as in RFA to achieve linear complexity;
• On the other hand, its expressiveness is significantly improved towards RA via the following modifications:
  • The proposal distribution is data-dependent so that LARA can be adaptive with respect to the contextual information;
  • LARA adopts multiple proposal distributions, which can be combined in a query-specific manner.

LARA takes the following form $$ \begin{align} \mathsf{LARA}\left(\mbq_{n},\mbK,\mbV\right) &= \frac{\sum_{c=1}^C\alpha_{nc}(\omega_c)\frac{p_n(\omega_c)}{q_c(\omega_c)} f_n(\omega_c)}{\sum_{c=1}^C\alpha_{nc}(\omega_c)\frac{p_n(\omega_c)}{q_c(\omega_c)}}.\label{eqn:lara} \end{align} $$ Here,

• $q_1(\omega), \dots, q_C(\omega)$ are $C$ different proposals that depend on different query and key information;
• $\{\alpha_{nc}(\cdot)\}_{c=1}^C$ is a set of weights that controls the contribution of different proposals, which is exclusive to each query and satisfies $\sum_{c=1}^C \alpha_{nc}(\omega) = 1$;
• as long as $C$ is smaller than $N$, the computational complexity of LARA is linear, that is, $\mathcal{O}(CN+CM)$.

Remark: We provide a detailed discussion about the parameterization of our proposal distributions in Appendix G.3 of our paper. To summarize, we find the key is to let different proposals depend on different sets of query information so that they could be as query-specific as possible. A good default is to divide the whole sequence into $C$ chunks, compute the mean of queries $\{\widetilde{\mbq}_c\}_{c=1}^C$ and keys $\{\widetilde{\mbk}_c\}_{c=1}^C$ within the same chunk, and set $q_c(\omega) = \mcN(\omega;\widetilde{\mbq}_c + \widetilde{\mbk}_c, \mathbf{I})$. We find this choice works well across various benchmarks.

A Unified View of LARA, RA, and RFA

LARA can be equivalently written in a similar way to RA and RFA. We spell it out here to see a systematic comparison among RA, LARA, and RFA: $$ \begin{align} \mathsf{RA}\left(\mbq_{n},\mbK,\mbV\right) &= \frac{\xi(\mbq_n,\omega_n)^\top \sum_{m=1}^M\xi(\mbk_m, \omega_n) \mbv_{m}^{\top}}{ \xi(\mbq_n,\omega_n)^\top \sum_{m'=1}^M\xi(\mbk_{m'}, \omega_n)}, &&\textcolor{keywords}{\omega_n \sim p_n(\omega)}\notag\\ \mathsf{LARA}\left(\mbq_{n},\mbK,\mbV\right) &= \frac{\sum_{c=1}^C \textcolor{strings}{\alpha'_{nc}(\omega_c)} \xi(\mbq_n,\omega_c)^\top \sum_{m=1}^M\xi(\mbk_m, \omega_c) \mbv_{m}^{\top}}{\sum_{c=1}^C \textcolor{strings}{\alpha'_{nc}(\omega_c)} \xi(\mbq_n,\omega_c)^\top \sum_{m=1}^M \xi(\mbk_{m}, \omega_c)}, &&\textcolor{keywords}{\omega_c \sim q_c(\omega)}\notag\\ \mathsf{RFA}\left(\mbq_{n},\mbK,\mbV\right) &= \frac{ \sum_{s=1}^S\xi(\mbq_n,\omega_s)^{\top}\sum_{m=1}^M\xi(\mbk_m, \omega_s)\mbv_{m}^{\top}}{\sum_{s=1}^S \xi(\mbq_n,\omega_s)^{\top}\sum_{m'=1}^M\xi(\mbk_{m'}, \omega_s)}, &&\textcolor{keywords}{\omega_1,\dots,\omega_S \sim \mcN(\omega;0, \mathbf{I})} \notag \end{align} $$ where we denote $\alpha'_{nc}(\omega_c) \coloneqq \alpha_{nc}(\omega_c)\mcN(\omega_c;0, \mathbf{I})/q_c(\omega_c)$ to simplify the notation. Note that their major difference lies in the choice of sampling distributions.
LARA is not designed to be a simple interpolation between RA and RFA; instead, it is a generalized estimation framework that includes both RA and RFA as its special cases. To see this,

• LARA is equivalent to RA if $C = N$, $q_n(\omega) = p_n(\omega)$ and $\alpha_{nc}(\omega) = \delta_{nc}$ (that is, $\alpha_{nc}(\omega) = 1$ if $n = c$ and $0$ otherwise);
• LARA is equivalent to RFA if $q_c(\omega) = \mcN(\omega;0,\mathbf{I})$ and $\alpha_{nc}(\cdot)$ is constant for all $c = 1,\dots,C$ and $n = 1,\dots,N$.

With general proposals and weighting functions, LARA approximates softmax attention in a query-specific manner as in RA while achieving linear complexity as in RFA, effectively combining the advantages of both estimators. It is also easy to implement with a couple of lines of code.

Experimental Results

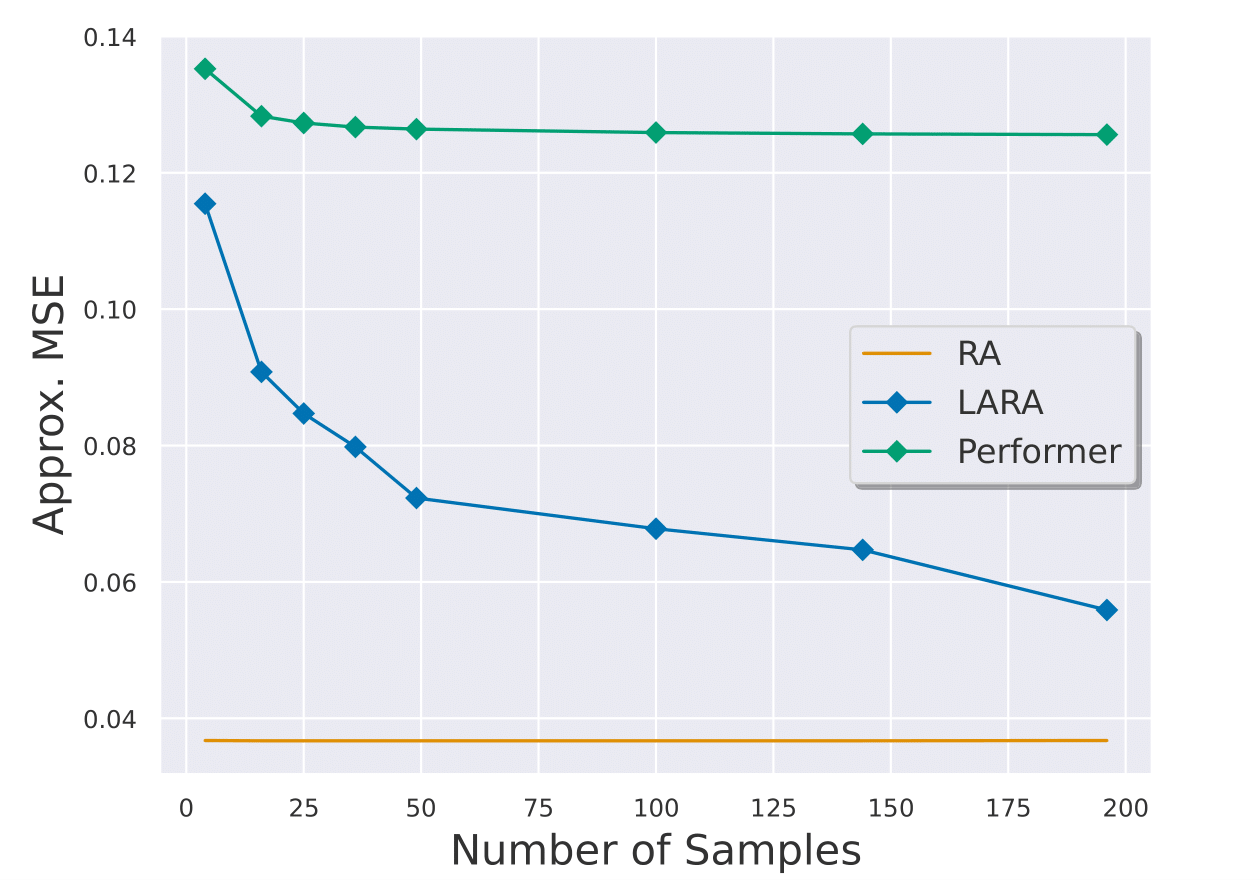
To demonstrate the effectiveness of our approach, we first visualize the approximation error of LARA to the true softmax attention outputs. Our unbiased estimate, RA, achieves the lowest MSE among these three methods and gets very close to the true softmax attention; RFA (Performer) soon plateaus at large approximation error and does not improve even with more samples, possibly due to low sample efficiency. On the other hand, LARA exhibits much lower MSE than RFA and the approximation error continually decreases as the number of proposals increases.

Mean Squared Error (MSE) between the true softmax attention and different RF approximations under different numbers of samples (lower is better), which are evaluated on DeiT.

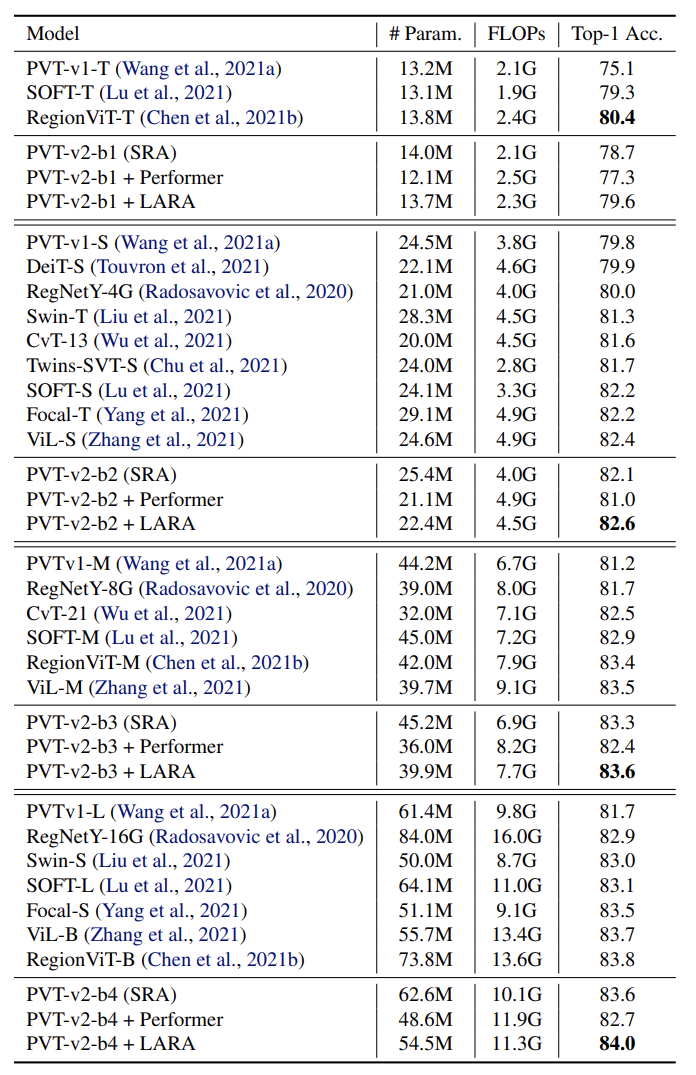
We further verify the improved performance of LARA by conducting experiments across a wide range of data modalities, including images, videos, natural language texts, and a long-sequence benchmark. From the Table below, we observe that

• RA performs competitively with conventional softmax attention, and
• LARA greatly improves the performance of RFA and significantly reduces the performance gap between RFA and softmax attention.

Model	Complexity	Image Classification on ImageNet (🠅)	Video Recognition on SSv2 (🠅)	Machine Translation on WMT (🠅)	Long Range Arena suite (🠅)
Softmax	$\mathcal{O}(N^2)$	79.9	66.5	27.5	59.08
RA	$\mathcal{O}(N^2)$	80.0	64.9	27.8	59.30
RFA	$\mathcal{O}(N)$	74.3	53.1	23.7	57.63
LARA	$\mathcal{O}(N)$	79.5	63.7	27.0	59.12

LARA also enjoys much better scalability and could achieve SOTA results for image classification when applying it to advanced transformer architectures.

SOTA results on ImageNet-1k across various model architectures.

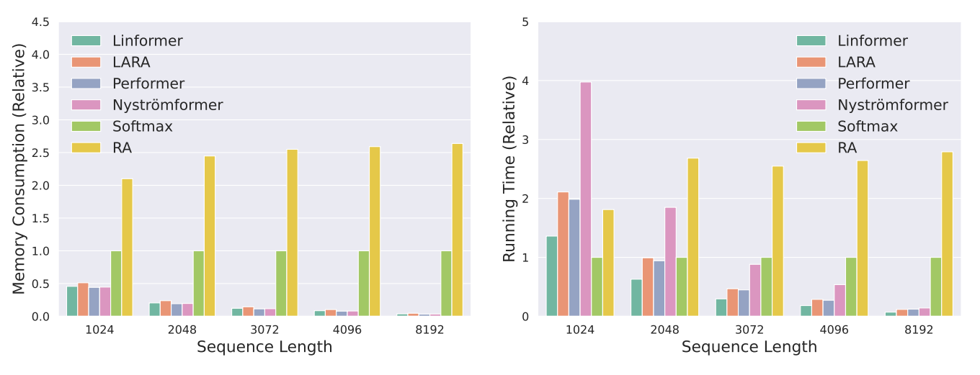
Finally, we evaluate the empirical efficiency of different attention methods. We note that RA runs almost twice slower than softmax attention, while its linear variant LARA runs much faster and brings marginal computational overheads compared to RFA.

Empirical memory consumption (left) and running time (right) of different attention mechanisms under different sequence lengths. Metrics are measured relative to the true softmax attention.

Conclusion and Limitation

In this work, we generalize the random feature attention (RFA) algorithm in two aspects:

• On the one hand, we generalize the unbiased kernel estimation (RFA) to unbiased attention estimation (RA);
• On the other hand, we uncover the self-normalized importance sampling nature of RFA and propose a general framework LARA that includes both RA and RFA as its special cases.

LARA greatly improves the performance of RFA while also maintaining its efficiency of RFA. Our framework provides a novel perspective for understanding and improving RF-based attention approximation, which is also orthogonal to most previous work. At the same time, there are several limitations of our approach:

• The choice of proposal distributions is sub-optimal. Although our modeling strategy enables a query-specific treatment as desired in RA, it needs to evaluate all the $C$ samples for each key-value pair, incurring a potential waste of computing. Future work might include more sophisticated implementations that use variable sample sets for different key-value pairs.
• Currently, LARA is still a biased (but consistent) estimator for softmax attention. It would be interesting to adopt advanced sampling strategies (e.g., Markov chain Monte Carlo (MCMC), etc.) to derive lower-bias lower-variance estimators.
• The proposal distribution should be carefully designed when dealing with auto-regressive modeling since it is non-trivial to apply the causal masking mechanism to LARA as in conventional softmax attention. Adapting the importance sampling formulation of LARA to support arbitrary auto-regressive modeling is also an interesting research direction.